3.2.1.2. Hibridación y geometría molecular

Moléculas poliatómicas: hibridación de orbitales.

Considérese ahora la molécula de agua. La configuración electrónica del oxígeno es 2s² 2px² 2py¹ 2pz¹. Los dos electrones de los orbitales 2py y 2pz pueden aparearse y formar enlaces σ con los orbitales 1s de los hidrógenos. Como estos orbitales p son perpendiculares entre sí, dichos enlaces σ deberían presentar esa misma separación. Sin embargo, el ángulo H-O-H es de 104.5º. Algo similar ocurre con la molécula de amoniaco. Los tres electrones de los orbitales p formarían sendos enlaces σ con los tres átomos de hidrógeno, y la separación también tendría que ser de 90º, cuando experimentalmente se conoce que dicho valor es de 107º. ¿Constituyen estas excepciones errores de la Teoría del Enlace de Valencia? Esta cuestión se resuelve a continuación.

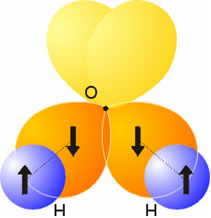
Explicación errónea de la molécula de agua.

Una deficiencia aparente de esta teoría es el no poder explicar la tetravalencia del carbono, es decir, su habilidad para formar cuatro enlaces. La configuración del átomo de carbono en su estado fundamental es 1s²2s²2px¹2py¹, la cual sugiere que dicho átomo sólo puede formar dos enlaces en lugar de cuatro. Para que el carbono forme cuatro enlaces debe alcanzar su estado de valencia. El estado de valencia de un átomo en una molécula es el estado electrónico de ese átomo en el cual se puede combinar con los otros átomos para formar la molécula sin que sea necesaria ninguna reorganización electrónica adicional. Así pues, para que el C forme cuatro enlaces debe tener cuatro electrones en cuatro orbitales de la misma energía (estado V4), con los espines orientados al azar. Esos orbitales son los híbridos sp3.

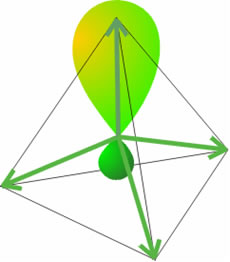
Orbitales híbridos sp³.

Así pues, para pasar del estado fundamental al estado de valencia es preciso promocionar un electrón del orbital 2s al 2p, y luego hibridar o mezclar los cuatro orbitales. La hibridación no es más que una mezcla o combinación lineal de orbitales atómicos puros (s y p, en este caso). La combinación lineal de un orbital 2s y de los tres orbitales 2p conduce a la formación de cuatro orbitales híbridos equivalentes:

h1 = s + px + py + pz
h2 = s – px + py – pz
h3 = s – px – py + pz
h4 = s – px – py – pz

Como resultado de esta interferencia entre los orbitales, cada orbital híbrido consiste en un lóbulo más abultado que el otro y que apunta directamente hacia un vértice de un tetraedro regular. El ángulo entre los orbitales híbridos corresponde a los ángulos de un tetraedro y tiene un valor de 109,4°. Como cada uno de estos orbitales híbridos se ha formado a partir de un orbital s y 3 orbitales p se denomina orbital híbrido sp3. Ahora resulta más sencillo describir la formación de la molécula AB4 desde el punto de vista de la Teoría del Enlace de Valencia. Cada uno de los orbitales híbridos que resultan tras la promoción en el átomo A contiene 1 electrón desapareado, que se aparea con el electrón que ocupa un orbital 1s de cada átomo de hidrógeno, originando un enlace σ que apunta hacia uno de los vértices de un tetraedro. Como cada orbital sp3 presenta la misma "composición", los cuatro híbridos son idénticos, salvo sus orientaciones en el espacio.

Existen otros tipos de orbitales híbridos que se emplean para explicar las geometrías de otras especies químicas mediante la teoría del enlace de valencia. Así, las combinaciones lineales de un orbital s con dos orbitales p conduce a los híbridos sp2 que sirven para explicar la geometría de las moléculas trigonales planas, como el BF3. La combinación lineal de un orbital s y uno p conduce a la formación de dos orbitales híbridos sp de geometría lineal. En la siguiente tabla se representan distintos tipos de orbitales híbridos y sus geometrías.

Orbitales híbridos y sus geometrías.

Número de coordinación	Distribución	Orbital híbrido
2	Lineal angular	sp, pd, sd sd
3	Plana triangular Pirámide trigonal	sp2, p2d pd2
4	Tetraedro Plana cuadrada	sp3, sd3 p2d2, sp2d
5	Bipirámide trigonal Pirámide tetragonal Plana pentagonal	sp3d, spd3 sp2d2, sd4, pd4, p3d2 p2d3
6	Octaedro	p3d2

Puedes revisar el tema de hibridación aqui (en inglés)