3.2.1.1 Teoría del Enlace de Valencia

En la actualidad existen dos teorías para explicar el enlace covalente: la Teoría del Enlace de Valencia y la Teoría de Orbitales Moleculares. Es preciso hacer notar que ninguna de las dos teorías es "mejor" que la otra, y que cada una de ellas puede ser más adecuada en función del parámetro, del cálculo o de la propiedad que se esté estudiando. Así, por ejemplo, si se trata de determinar la geometría molecular o la energía de disociación, propiedades del estado fundamental de la molécula, es más conveniente emplear la Teoría del Enlace de Valencia. En cambio, si se trata de explicar las propiedades espectroscópicas, es preferible emplear la Teoría de Orbitales Moleculares. En realidad ambas teorías son incluso complementarias, hasta tal punto que no utilizar ambas supondría limitar las herramientas disponibles para el estudio del enlace.

La Teoría del Enlace de Valencia (T.E.V.)

La Teoría del Enlace de Valencia fue la primera teoría, basada en la mecánica cuántica, que se desarrolló para explicar el enlace en las moléculas covalentes. Se puede considerar que expresa el concepto de Lewis del enlace en términos de las funciones de ondas. En 1927, Heitler y London propusieron un tratamiento mecano-cuántico para la molécula de hidrógeno, que fue posteriormente desarrollado por investigadores como Pauling y Slater, entre otros. Lo que aparece a continuación es un resumen del trabajo de Pauling y Coulson.

Como primera aproximación, considérense dos átomos de hidrógeno que se encuentran muy separados entre sí, a distancia infinita, de forma que no hay interacción posible entre ellos. La función de onda que describe al sistema será igual al producto de las funciones de onda que describen a cada átomo por separado:

Ψ = φ_A(1)φ_B(2)

donde φA y φB representan a los orbitales 1s de cada átomo de hidrógeno. Cuando se resuelve la ecuación de ondas en función de la distancia de separación entre los átomos, se obtiene un valor de la energía de -24 kJ/mol y una distancia de equilibrio de 90 pm. Los valores experimentales para esta molécula son –458 kJ/mol y 74 pm, respectivamente, lo que indica que esta aproximación dista mucho de representar la situación real.

Una mejora de dicha función, sugerida por Heitler y London, consiste en suponer que los electrones no pueden ser asignados de manera taxativa a los núcleos A y B. Cuando los átomos se aproximan hasta la distancia de equilibrio, no es posible distinguir si el electrón 1 está ligado al átomo A o al átomo B, y lo mismo sucede con el electrón 2. Así pues, una descripción del sistema igualmente válida es la que representa la función de onda Ψ = φ_A(2)φ_B(1), en la cual el electrón 2 está en el átomo A y el electrón 1 en el átomo B. Como ambas funciones son igualmente probables, la mejor función que describe al sistema resulta de una combinación lineal de ambas:

Ψ = φ_A(1)φ_B(2) + φ_A(2)φ_B(1)

Los valores de energía y distancia que se obtienen en este caso son -303 kJ/mol y 86.9 pm. Aunque estos valores aún están lejos de los correspondientes a la molécula real, sí se acercan más que los anteriores. Esta aproximación suele llamarse de intercambio, pues se basa en la posibilidad de que los electrones cambien de núcleo en lo que a asignaciones se refiere.

Una mejora posterior hace uso de la carga nuclear efectiva. Aunque tenemos dos electrones y dos núcleos, cada electrón apantalla al otro en cierto grado, por lo que el empleo de Zef en φ_A y φ_B podría mejorar el cálculo. Y así sucede, como se observa en la tabla

Energías y distancias de equilibrio para las funciones de onda de Enlace Valencia (Molécula de hidrógeno)

Función de onda	Energía (kJ/mol)	Distancia (pm)
Ψ = φA(1)φB(2)	24	90
Ψ = φA(1)φB(2) + φA(2)φB(1)	303	86.9
Inclusión de Zef	365	74.3
Contribución iónica	388	74.9
Valores Experimentales	458	74.1

Pero aún es posible incluir una corrección adicional que supone que en algún momento los dos electrones puedan “pertenecer” a un único átomo (A o B) simultáneamente, en lo que comúnmente se denomina la contribución iónica. Aunque es una situación extrema, no lo es menos el suponer que los dos electrones van a estar siempre uno con cada núcleo. Así pues, lo que esto presupone es la existencia de una parte iónica en un enlace covalente:

H-H  H⁺ H^-  H^- H⁺
covalente iónica        

Entonces puede escribirse la siguiente función de onda molecular:

Ψ = φ_A(1)φ_B(2) + φ_A(2)φ_B(1) + λ φ_A(1)φ_A(2) + λ φ_B(1)φ_B(2)

en la que los dos primeros términos representan la estructura covalente y los dos siguientes las estructuras iónicas. Como los dos electrones tienden a repelerse entre sí, la probabilidad de encontrar a los dos sobre el mismo núcleo es inferior y por eso la contribución iónica pesa menos que la covalente ( λ < 1). Esta ecuación puede escribirse también de la forma siguiente:

Ψ = φ_cov + λ φ _H⁺ H^- + λ φ _H^- H⁺

Resulta obvio que esta función de onda puede modificarse por adición de términos que acerquen los cálculos hasta los valores experimentales. De hecho, se ha publicado una función Ψ con 100 términos que acerca el valor de la energía hasta el límite de 0.01 kJ/mol.

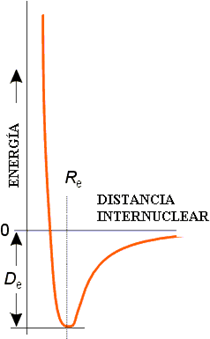
Variación de la energía frente a la distancia internuclear.

La función de onda Ψ representa un enlace σ (sigma). Este orbital presenta simetría cilíndrica alrededor del eje internuclear. La siguiente figura muestra la variación de la energía potencial para la molécula de H₂ en función de la distancia internuclear. Esta curva presenta un mínimo que corresponde a la distancia de equilibrio (o de enlace) en esta molécula.

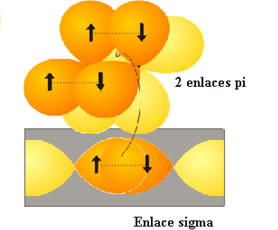
Enlaces s y p para la molécula de N₂.

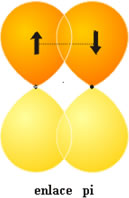
Enlace p.