Las estructuras de los sólidos
Introducción
La característica principal de un sólido, ya sea metálico o ionico, es la disposición de sus átomos e iones que conducen a la formación del cristal. En estas sustancias no existe un enlace covalente direccional predominante, sino que cada uno de los átomos se considera enlazado al resto del cristal. Esta disposición suele representarse por medio de esferas sólidas. Un cristal de un elemento o de un compuesto puede considerarse, desde el punto de vista formal de su construcción, como la repetición regular de unidades asimétricas, que pueden ser átomos, moléculas o iones. Esa unidad se denomina celda unidad. La Figura 1 muestra un ejemplo de celda unidad para una sólido bidimensional. Las dos unidades que aparecen sombreadas representan sendas celdas unidades, ya que su traslado a lo largo del plano conduce a la formación de la red. Sin embargo, suele emplearse como celda unidad aquella de más alta simetría y de menor tamaño, lo que en este caso sucede para (a).
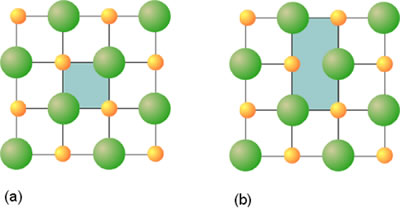
Figura 1. Celda unidad para un sólido bidimensional.
La mayoría de sólidos metálicos e iónicos están formados por átomos o iones que desde un punto de vista práctico pueden considerarse como esferas. Sin la existencia de enlace covalente direccional, estas esferas podrían empaquetarse de forma tan compacta como permitiera la geometría, de forma que el espacio que no se ocupara entre ellas sea el mínimo. Esto es lo que se denomina empaquetamiento compacto. En esta situación, y cuando se trata de átomos idénticos, cada esfera está directamente rodeada por doce esferas vecinas. Este número se denomina número de coordinación.
Empaquetamiento de esferas
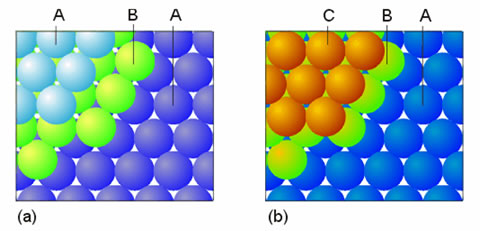
Figura 2. Los dos politipos de empaquetamiento compacto. (a) Hexagonal, (b) Cúbico
La formación de estructuras compactas puede visualizarse de manera simple. La primera capa consiste en esferas tangentes entre sí de tal forma que cada una de ellas está rodeada de otras seis en dicha capa. La segunda capa se construye ubicando las esferas sobre los puntos de tangencia de las esferas de la primera capa. Es en la formación de la tercera capa donde surgen diferencias, que conducen a la formación de politipismo: estructuras idénticas en dos dimensiones pero distintas en la tercera. El número de coordinación es el mismo (12) en ambos politipos.
Empaquetamiento Compacto
Uno de los politipos se forma cuando las esferas de la tercera capa ocupan posiciones sobre las esferas de la primera, en lo que se denomina estructura ABAB..., donde A representa una capa y B representa otra capa (Figura 2a). Esto supone la aparición de una celda unidad hexagonal (Figura 3 a), por lo que se denomina empaquetamiento compacto hexagonal. El segundo politipo se forma cuando las esferas de la tercera capa ocupan posiciones sobre los huecos que se forman en la primera capa (Figura 2b). En este caso la disposición conduce a una distribución ABCABC..., lo que indica que hay tres tipos de capas en lo que a su ubicación respectiva se refiere. La celda unidad correspondiente presenta simetría cúbica (Figura 3b), lo que explica su denominación: empaquetamiento cúbico compacto.
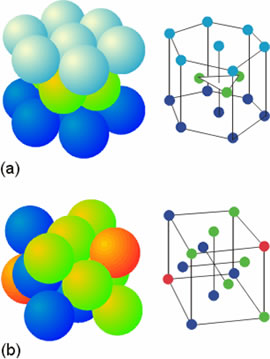
Figura 3. Celdas unidad de los empaquetamientos compactos hexagonal (a) y cúbico (b).
Huecos en estructuras empaquetadas
Una de las características de los empaquetamientos es el tipo de huecos que se genera entre las esferas. Para una estructura compacta, la porción de espacio no ocupada, es decir, la cantidad de espacio libre por huecos, es el 26 % del total. Existentes dos tipos de huecos: el hueco octaédrico y el hueco tetraédrico.
El hueco octaédrico aparece entre dos triángulos de esferas que están opuestos entre sí (Figura 4). En una estructura compacta de N átomos existen N huecos octaédricos. Además, cada hueco presenta simetría octaédrica, ya que los seis átomos que lo forman se disponen en los vértices de un octaedro (Figura 4). Si cada esfera tiene un radio r, puede demostrarse fácilmente que un hueco de estas características puede acomodar otra esfera de radio 0.414r.
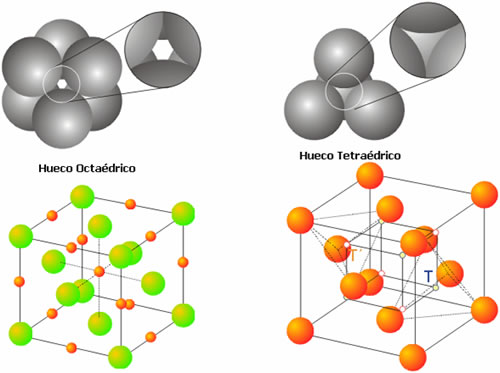
Figura 4. Huecos Octaédricos y Tetraédricos
El hueco tetraédrico aparece como consecuencia de la ubicación de una esfera sobre el triángulo que forman otras tres (Figura 4). Existen dos tipos de agujeros tetraédricos, dependiendo de que el vértice del mismo está orientado hacia arriba o hacia abajo (Figura 4). En un empaquetamiento compacto existen N huecos de cada tipo, para dar un total de 2N huecos tetraédricos. En una estructura de este tipo, con átomos de radio r, el hueco tetraédrico puede acomodar una esfera de radio igual o inferior a 0.225r.

No hay comentarios:
Publicar un comentario